Полиномиальная регрессия

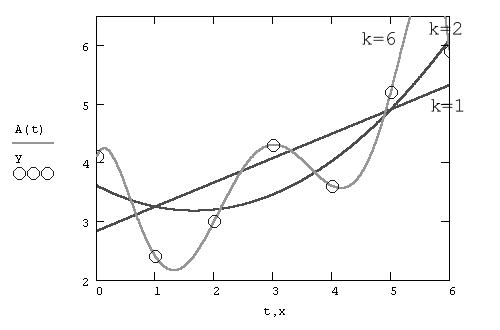
Полиномиальная регрессия означает приближение данных (x_i,y_i) полиномом k–й степени A(x)=a+b×x+c×x²+d×x³+…+h×x^k. При k=1 полином является прямой линией (см. предыдущий раздел линейная регрессия), при k=2 – параболой, при k=3 – кубической параболой и т. д. Как правило, на практике применяются k<5.  Регрессия полиномами разной степени (для разных k) иллюстрируется в виде коллажа на рис. снизу.

Замечание 1. Для построения регрессии полиномом k–й степени необходимо наличие по крайней мере (k+1) точек данных.

Замечание 2. Помимо приближения массива данных одним полиномом, регрессию можно проводить также отрезками полиномов. В этом случае имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они криволинейной формы) нескольких полиномов. Регрессия одним полиномом эффективна, когда множество точек выглядит приблизительно как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.