 Анализ Данных
> Интерполяция
Анализ Данных
> Интерполяция
Интерполяция и экстраполяция
В огромном количестве численных методов используются алгоритмы интерполяции. Вообще говоря, вычислительная математика - это наука о дискретных представлениях функций. Именно конечный набор значений y(xi) представляет на компьютерном языкематематическую абстрацию - непрерывную функцию y(x). Задача интерполяции функции одной переменной состоит в замене дискретной зависимости y(xi), т.е. N пар чисел (xi,yi), или, по-другому, узлов, некоторой непрерывной функцией y(x). При этом основным условием является то, что функция y(x) должна проходить через точки (xi,yi), т. е. y(xi)=yi ,i=1...N, а также возможность вычислить значение y(x) в любой точке, находящейся между узлов.
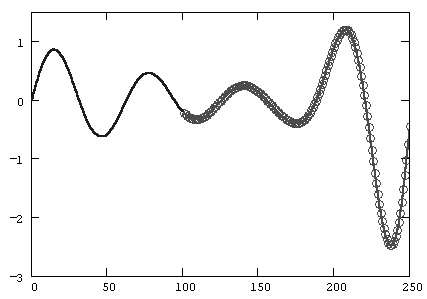 Когда искомое значение y(x) вычисляется в точке x, которая находится между
каких-либо из узлов xi, говорят об интерполяции, а
когда точка x лежит вне границ интервала, включающего все
xi - об экстраполяции функции y(x).
Когда искомое значение y(x) вычисляется в точке x, которая находится между
каких-либо из узлов xi, говорят об интерполяции, а
когда точка x лежит вне границ интервала, включающего все
xi - об экстраполяции функции y(x).
На рисунке по множеству точек (xi,yi), обозначенных кружками, построена как интерполирующая (при x>100), так и экстраполирующая их функция (при x<100). Интерполяция-экстраполяция показаны на рис. сплошной кривой.
Разделы: