СПЕКТРАЛЬНЫЙ АНАЛИЗ
Математический смысл преобразования Фурье состоит в представлении сигнала y(x) в виде бесконечной суммы синусоид вида F(v) sin(vx). Функция F(v) называется преобразованием Фурье, или интегралом Фурье, или Фурье-спектром сигнала. Ее аргумент v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводит спектр F(v) в исходный сигнал y(x). Согласно определению,
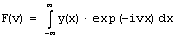 .
.Как видно, преобразование Фурье является существенно комплексной величиной, даже если сигнал действительный.
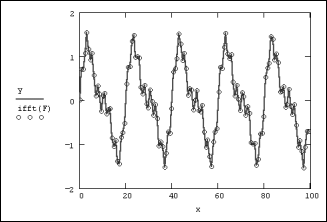
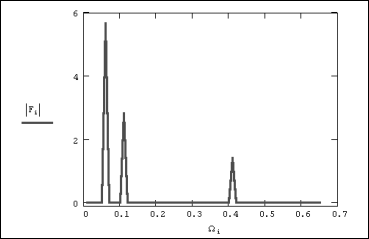
Пример расчета Фурье-спектра для суммы трех синусоидальных сигналов разной амплитуды (показанных в виде сплошной кривой на рис.1), приведен на рис.2. Расчет проводится по N=128 точкам, причем предполагается, что интервал дискретизации данных yi равен D=100/N. Обратите внимание, что результаты расчета мы представили в виде модуля Фурье-спектра (рис.2), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра с определением синусоид:
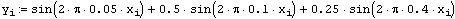 .
.
-
Основные понятия (стационарность, энергетические и Фурье- спектры и т.п.).
-
Алгоритмы вычисления энергетических спектров данных эксперимента (прямой и косвенный).
-
Численный метод Фурье-преобразования (БПФ).
-
Частота Найквиста.
-
Влияние конечности интервала выборки и методы его устранения.
-
Явление маскировки частот.
-
Оценка погрешности вычисления спектров.
-
Cпектральный анализ нестационарных процессов. СВАН-диаграммы.